5. Vectors

a. Definition, Magnitude and Direction

2. Displacements

Vectors are often drawn between two points in order to show a change of position or displacement. In particular, if something moves from point \(P=(p_1,p_2)\) to a point \(Q=(q_1,q_2)\), this change in position is commonly denoted by the displacement vector: \[ \overrightarrow{PQ}=Q-P=\left\langle q_1-p_1,q_2-p_2\right\rangle \] Here, \(P\) is the tail of the vector while \(Q\) is the tip of the vector.

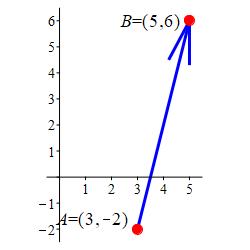
Suppose you trace a line segment which starts at the point \(A=(3,-2)\) and ends at the point \(B=(5,6)\). What displacement vector describes this motion?

Subtract the coordinates of the initial position from those of the final position. The resulting displacement vector is \[ \overrightarrow{AB}=B-A=(5,6)-(3,-2)=\left\langle2,8\right\rangle \] The picture gives a graphical representation of this vector.

Find the displacement vector from \(P=(1,3)\) to \(Q=(4,7)\). Plot it.

\(\overrightarrow{PQ}=\left\langle3,4\right\rangle\)

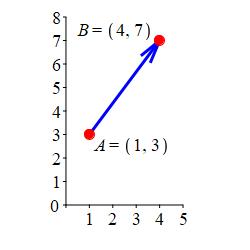
The displacement vector is: \[ \overrightarrow{PQ}=Q-P=(4,7)-(1,3) =\left\langle3,4\right\rangle \] We plot the points \(P=(1,3)\) and \(Q=(4,7)\) and connect the dots.

5. Vectors

a. Definition, Magnitude and Direction

2. Displacements

Heading